Abstract The speed of light, denoted by the symbol c, is one of the most important and universally accepted constants in physics. It has played a pivotal role in shaping modern theories of space, time, and energy, from the foundations of electromagnetism to the principles of relativity and quantum mechanics. In this thesis, we explore the nature of the speed of light, its historical development, its role in fundamental physics, and the implications it holds for our understanding of the universe. We further discuss the experimental methods used to measure this constant and the impact it has on the limits of physical phenomena.
Historical Background
Early Concepts of Light
The understanding of light has evolved through the ages, starting from ancient civilizations who regarded light as a fundamental element of nature. Ancient Greek philosophers like Pythagoras and Plato speculated on the nature of light, but it was only with the works of Isaac Newton and Christiaan Huygens in the 17th century that the wave-particle duality of light began to be seriously considered.
First Measurements of Light Speed
Ole Rømer, a Danish astronomer, made the first quantitative estimate of the speed of light in 1676, by observing the eclipses of Jupiter’s moon Io. Rømer deduced that light takes time to travel over cosmic distances. His estimation of 220,000 km/s was a pioneering attempt, although it differed from today’s accepted value of 299,792,458 m/s due to the lack of accurate measurements at the time.
In the 19th century, Armand Fizeau and Léon Foucault developed more precise experimental techniques to measure the speed of light using terrestrial equipment. These efforts paved the way for a better understanding of light as an electromagnetic wave.
The Nature of Light and Electromagnetism
James Clerk Maxwell’s Contributions
The most significant breakthrough in understanding light came with James Clerk Maxwell’s equations, formulated in 1864. Maxwell demonstrated that light is an electromagnetic wave that propagates through space. He derived a set of equations showing that electric and magnetic fields oscillate perpendicular to each other, and the speed of these waves could be determined by fundamental constants of electricity and magnetism.
The equation for the speed of light in a vacuum a vacuum is given by:
c=1/√μ0ε0
where:
- μ₀ is the permeability of free space,
- ε₀ is the permittivity of free space.
Maxwell’s theory not only provided a theoretical basis for the speed of light but also established that this speed is constant, regardless of the motion of the observer or the source.
The Role of Ether in Light Propagation
In the 19th century, it was believed that light required a medium (called the luminiferous ether) to propagate, much like sound waves need air. However, experiments by Michelson and Morley in 1887 attempted to detect this ether but failed. Their negative results led to the conclusion that light does not need a medium for propagation and that its speed remains constant in a vacuum.
The Speed of Light and Relativity
Einstein’s Theory of Special Relativity
In 1905, Albert Einstein revolutionized our understanding of space and time with his theory of special relativity. A cornerstone of this theory is the constancy of the speed of light for all observers, irrespective of their relative motion. This postulate led to profound consequences, including time dilation, length contraction, and the famous energy-mass equivalence formula:
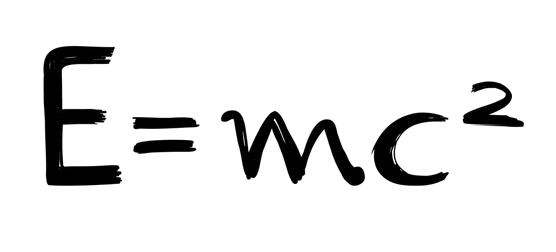
In Einstein’s formulation, the speed of light plays a central role in determining how objects behave at relativistic speeds (those approaching the speed of light). According to relativity, no object with mass can travel at the speed of light, as doing so would require infinite energy. Thus, c represents the ultimate speed limit in the universe.
Lorentz Transformation and Time Dilation
The Lorentz transformation equations describe how measurements of time and space change for observers moving at constant velocities relative to each other. These transformations show that as an object approaches the speed of light, time appears to slow down for the moving object relative to a stationary observer. This effect is known as time dilation and is given by the equation:
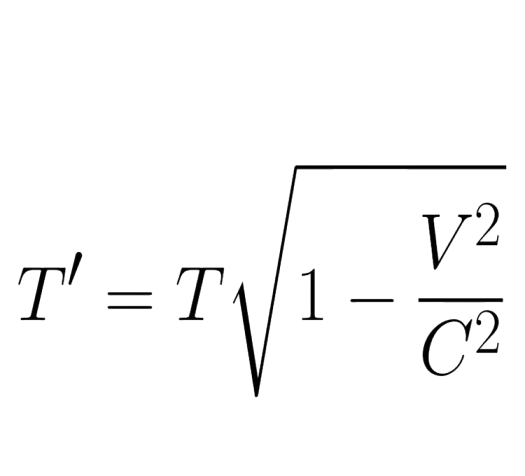
where:
- T is the proper time,
- T’ is the dilated time,
- v is the velocity of the moving object.
This profound relationship between the speed of light and the passage of time highlights the non-intuitive nature of spacetime at relativistic speeds.
Quantum Mechanics and the Role of Light
The Photon Model and Wave-Particle Duality
The development of quantum mechanics revolutionized the understanding of light, revealing that it behaves both as a wave and as a particle, a concept known as wave-particle duality. This duality emerged from the failure of classical physics to explain certain phenomena involving light and energy, such as blackbody radiation and the photoelectric effect. Classical physics treated light solely as a wave, as established by James Clerk Maxwell’s electromagnetic theory, but experiments at the beginning of the 20th century revealed a more complex nature of light.
1. Wave Theory of Light
Before the quantum revolution, the wave theory of light was dominant. According to Maxwell’s equations, light is an electromagnetic wave that propagates through space with a constant speed, c. This wave description accounted for many properties of light, including interference and diffraction. Light’s behavior as a wave is characterized by its wavelength (λ), frequency (f), and speed (c), with the relationship:
c=λf
Here, λ is the wavelength of the light wave, and f is its frequency.
However, certain phenomena, such as the emission of light from heated objects (blackbody radiation) and the photoelectric effect, could not be explained by this classical wave description of light. These problems led to the development of quantum mechanics, which introduced the concept of light also behaving as a particle.
2. Einstein and the Photoelectric Effect: The Birth of the Photon
2.1 The Photoelectric Effect
In 1887, Heinrich Hertz discovered the photoelectric effect, where light striking a metal surface caused the emission of electrons. Classical wave theory predicted that the energy of emitted electrons should depend on the intensity (brightness) of light, regardless of its frequency. Furthermore, it was believed that there would be a time delay between the absorption of light and the emission of electrons.
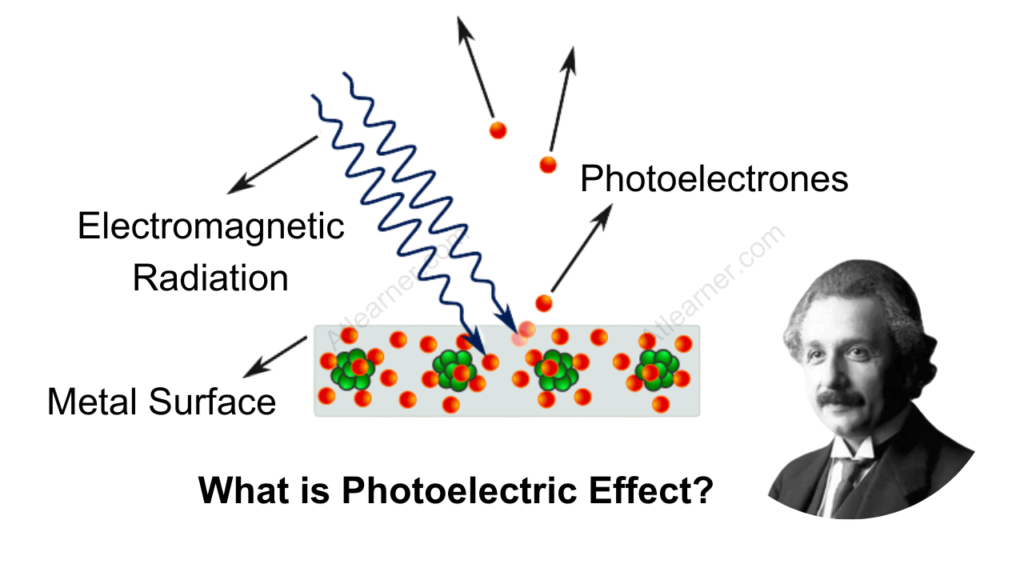
However, experiments showed that:
- The energy of emitted electrons depended on the frequency of light, not its intensity.
- There was no delay in the emission of electrons when the light frequency exceeded a certain threshold, no matter how low the light intensity.
- Light below a certain frequency, no matter how intense, could not eject electrons.
These results were inconsistent with the classical wave theory of light.
2.2 Einstein’s Photon Hypothesis
In 1905, Albert Einstein proposed a radical idea to explain the photoelectric effect, building on Max Planck’s earlier work on blackbody radiation. Planck had suggested that energy is quantized, meaning it is emitted or absorbed in discrete packets (quanta). Einstein extended this idea by proposing that light itself consists of individual particles, or quanta, later called photons. He suggested that each photon carries a discrete amount of energy proportional to its frequency:
E=hf
Where:
- E is the energy of the photon,
- h is Planck’s constant (6.62607015×10−34 joule-hertz−1),
- f is the frequency of the light.
According to Einstein’s theory, when a photon strikes a metal surface, it transfers its energy to an electron. If the photon’s energy is greater than the work function (the minimum energy required to eject an electron from the metal surface), the electron is emitted instantly with kinetic energy given by:
Eₖ=hf−ϕ
Where:
- Eₖ is the kinetic energy of the emitted electron,
- hf is the energy of the photon,
- ϕ is the work function of the metal.
Einstein’s photon model explained all the experimental results of the photoelectric effect:
- The energy of emitted electrons depends on the light frequency, not intensity, because higher frequency photons carry more energy.
- Electrons are emitted immediately when the photon’s energy exceeds the work function, without delay.
- Below a certain threshold frequency, no electrons are emitted because the photons do not have enough energy to overcome the work function, regardless of intensity.
2.3 Contribution to Quantum Theory
Einstein’s explanation of the photoelectric effect was pivotal in establishing the quantum nature of light. His work was instrumental in developing the broader framework of quantum mechanics, which describes the behavior of particles on atomic and subatomic scales. In 1921, Einstein was awarded the Nobel Prize in Physics for his explanation of the photoelectric effect, recognizing its significance in the new quantum theory.
The photon concept was a radical departure from classical wave theory. While light behaves as a wave in phenomena like interference and diffraction, it also behaves as a particle in processes like the photoelectric effect. This duality is a central feature of quantum mechanics, not only for light but for all matter, as later demonstrated by Louis de Broglie in his matter-wave hypothesis.
3. Energy of a Photon: E=hf
The equation E=hf remains one of the most important relationships in quantum mechanics, linking the wave-like and particle-like properties of light. This equation implies that higher frequency light (such as ultraviolet or X-rays) has more energetic photons than lower frequency light (such as radio waves or infrared).
In terms of wavelength, since the speed of light is constant in a vacuum (c = 299,792,458 m/s), the frequency and wavelength of light are inversely related. The energy of a photon can also be expressed in terms of its wavelength:
E=hc/λ
Where:
- c is the speed of light in a vacuum,
- λ is the wavelength of light.
This relationship shows that shorter wavelengths (such as gamma rays) correspond to higher photon energies, while longer wavelengths (such as radio waves) correspond to lower photon energies.
4. Applications in Modern Technology
The particle nature of light has led to numerous technological advancements, particularly in fields like photovoltaics, lasers, and optical communication.
4.1 Photovoltaics
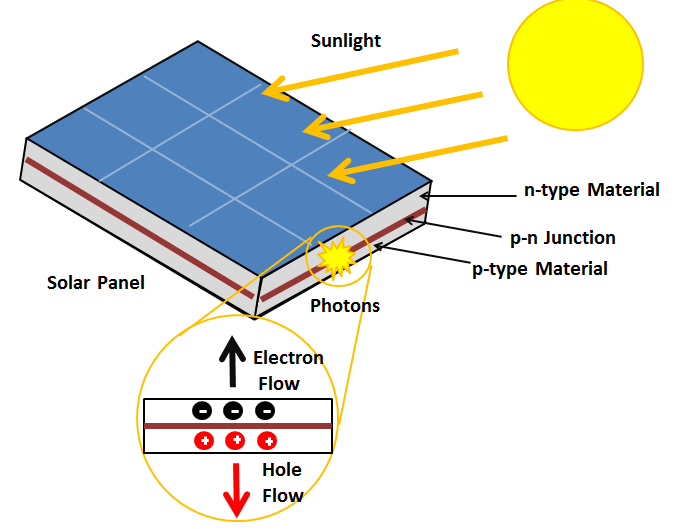
The principles of the photoelectric effect are directly applied in photovoltaic cells, which convert sunlight into electrical energy. In these cells, photons from sunlight strike a semiconductor material, usually silicon, and transfer their energy to electrons. This causes the electrons to jump to a higher energy level, creating an electric current. Photovoltaic cells are the basis of solar panels, which are used to generate renewable energy.
- The efficiency of solar cells depends on the material’s ability to absorb photons and the energy of those photons. Higher-energy photons (such as those from ultraviolet light) can potentially generate more electricity, but the material must also be able to absorb photons with lower energy (such as visible light) to maximize efficiency.
4.2 Lasers

Lasers (Light Amplification by Stimulated Emission of Radiation) are another application of the quantum theory of light. In a laser, photons are used to stimulate the emission of more photons in a controlled manner. The process relies on the interaction between light and the quantized energy levels of atoms or molecules in the laser medium.
- When an atom in the laser medium is excited by absorbing energy, it can return to a lower energy state by emitting a photon. If this photon encounters another excited atom, it can stimulate the emission of a second photon with the same energy, phase, and direction. This creates a coherent beam of light, characteristic of lasers.
- Lasers are used in many applications, including telecommunications (fiber-optic communication), medicine (laser surgery, eye treatments), and industry (cutting and welding materials).
4.3 Light Emitting Diodes (LEDs)
LEDs are semiconductor devices that emit light when an electric current passes through them. The process involves electrons recombining with electron holes in the material, releasing energy in the form of photons. The color (or wavelength) of the light emitted by an LED depends on the energy bandgap of the semiconductor material, which determines the energy of the emitted photons.
Heisenberg Uncertainty Principle and Its Implications for Light
The Heisenberg Uncertainty Principle is a fundamental concept in quantum mechanics, formulated by Werner Heisenberg in 1927. It asserts that certain pairs of physical properties, known as complementary variables, cannot be simultaneously measured with arbitrary precision. For light, this applies most directly to pairs like position and momentum, or equivalently, energy and time. Specifically, the principle states that the more precisely one of these variables is known, the less precisely the other can be known. This is expressed mathematically as:
Δx⋅Δp≥ℏ/2
Where:
- Δx is the uncertainty in position,
- Δp is the uncertainty in momentum,
- ℏ is the reduced Planck’s constant (h/2π).
In the context of light, which exhibits both wave-like and particle-like properties, the principle becomes particularly insightful. Photons, the quanta of light, are subject to this uncertainty, meaning that trying to precisely determine both a photon’s position and its momentum (which is related to its wavelength) is fundamentally limited.
Wave-Particle Duality and Light
To understand the uncertainty principle’s implications for light, it’s important to consider the wave-particle duality of light. Light exhibits characteristics of both waves and particles. As a wave, light is described by its wavelength (λ) and frequency (f), while as a particle, it can be considered in terms of photons, each with energy E=hf, where h is Planck’s constant. This dual nature directly affects how we measure and interact with light.
For instance, when we treat light as a wave, its wavelength and frequency can be measured precisely, but its position is highly uncertain because waves are spread out over space. Conversely, if we treat light as a particle (photon), we can localize its position, but this introduces uncertainty in its momentum (or wavelength). The Heisenberg Uncertainty Principle mathematically formalizes this trade-off.
Uncertainty in Position and Momentum
When applied to light, the uncertainty in position (Δx\Δx) and momentum (Δp\Δp) can be understood through experiments like the double-slit experiment, which demonstrates the wave-particle duality. If we attempt to pinpoint the precise path of a photon (position), the interference pattern that reveals its wave-like behavior disappears, because we lose information about the momentum. On the other hand, if we measure the momentum or wavelength of light precisely, we cannot determine the exact location of the photon.
For example, consider a beam of light passing through a narrow slit. The position of the photon becomes well-defined (as the slit confines its position), but this causes the beam to diffract, spreading out over a range of angles. The diffraction pattern illustrates the increased uncertainty in the photon’s momentum after passing through the slit.
Uncertainty in Energy and Time
In addition to position and momentum, the Heisenberg Uncertainty Principle also applies to energy and time. This is expressed as:
ΔE⋅Δt≥ℏ/2
Where:
- ΔE\Delta EΔE is the uncertainty in energy,
- Δt\Delta tΔt is the uncertainty in time.
In the case of light, this means that if the energy (or frequency) of a photon is measured precisely, there is a corresponding uncertainty in the time duration during which that measurement occurred. This is particularly relevant in high-energy phenomena such as the emission or absorption of photons, where extremely short bursts of light (such as those in femtosecond lasers) involve a high uncertainty in energy due to their limited duration.
Implications for Light and Quantum Optics
The Heisenberg Uncertainty Principle has profound implications in fields such as quantum optics and photonic technology. In technologies like lasers and quantum cryptography, the manipulation and measurement of photons are often constrained by the uncertainty principle. For example, in quantum cryptography protocols, like quantum key distribution (QKD), the principle ensures that any attempt to measure a quantum state (like the polarization of photons) disturbs the system, alerting the communicating parties to potential eavesdropping.
In laser physics, the uncertainty between energy and time becomes significant in designing highly precise lasers with short pulses. Femtosecond lasers, which emit pulses on the order of 10⁻¹⁵ seconds, must contend with energy uncertainty, limiting the precision with which the laser’s frequency can be controlled.
Uncertainty and Single-Photon Experiments
Modern experiments in quantum mechanics, particularly those involving single-photon sources, further explore the implications of the uncertainty principle. In these experiments, individual photons are isolated and their behavior studied. The uncertainty principle plays a crucial role in determining how much can be known about each photon’s trajectory and energy. For example, in quantum computing and quantum communication, understanding and controlling the uncertainty in photon properties is essential for encoding and transmitting quantum information.
Heisenberg’s Principle and Fundamental Limits in Measurement
At a deeper level, the Heisenberg Uncertainty Principle challenges the classical notion of determinism. In classical physics, knowing the initial conditions of a system allows for precise predictions about its future behavior. Quantum mechanics, however, introduces intrinsic limits to how much can be known about a system, even in principle. The behavior of light, governed by this uncertainty, highlights the fundamental probabilistic nature of quantum mechanics.
In the context of light, this means that no matter how sophisticated our measurement techniques become, there will always be a trade-off between the precision with which we can measure certain properties, like a photon’s position and momentum or its energy and time. This leads to a probabilistic description of light and other quantum particles, where the best we can do is predict the likelihood of finding a photon in a particular state, rather than determining its exact state.
Quantum Electrodynamics (QED) and the Speed of Light
Quantum Electrodynamics (QED) is the quantum field theory that describes how light interacts with charged particles, such as electrons, through the exchange of photons. It extends the classical understanding of electromagnetism to the quantum realm by explaining that electromagnetic forces are mediated by the exchange of virtual photons, which are carriers of the force between particles.
Richard Feynman, a key figure in the development of QED, introduced Feynman diagrams, a visual tool to represent these interactions. In these diagrams, charged particles exchange photons, either real or virtual, and the paths they take describe the probabilities of various outcomes in particle interactions. Virtual photons, unlike real photons, do not directly interact with detectors and exist only temporarily within the constraints of the Heisenberg Uncertainty Principle, facilitating force interactions over distance.
In QED, the speed of light, c, plays a critical role as it sets the maximum speed at which any information, including the interaction of forces, can travel. The value of c is woven into the fundamental structure of QED equations, ensuring that causality is preserved. The theory’s success in explaining phenomena like the anomalous magnetic moment of the electron and Lamb shift makes it a cornerstone of modern particle physics, providing precise predictions that agree remarkably with experimental results.
Modern Experimental Methods for Measuring the Speed of Light
Fizeau-Foucault Experiments Revisited
The determination of the speed of light is one of the most important achievements in experimental physics. Early measurements by Hippolyte Fizeau and Léon Foucault in the mid-19th century laid the groundwork for increasingly precise methods. Their experiments involved ingenious techniques using rotating mirrors, light beams, and interference patterns, which evolved into highly refined measurements over time. These methods became foundational, influencing later advances and contributing to the modern, ultra-precise value of the speed of light.
Fizeau’s Experiment (1849)
1. Basic Setup
Fizeau was the first to measure the speed of light on Earth using a terrestrial experiment. His experiment used a beam of light and a rapidly rotating toothed wheel. The setup involved reflecting light off a distant mirror and measuring the time it took for the light to travel to the mirror and back. The key components of his setup included:
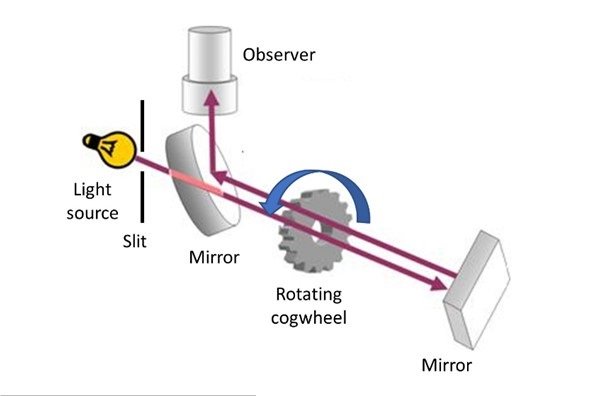
- A light source, typically an intense lamp.
- A toothed wheel that could be rotated at different speeds.
- A distant mirror positioned several kilometers away.
- An observer or detector to note when light passed through the gaps in the toothed wheel.
2. Working Principle
Fizeau directed a beam of light through the gaps between the teeth of a rotating wheel. The light then traveled to a distant mirror several kilometers away (in his case, approximately 8.6 km) and was reflected back toward the wheel. If the wheel was stationary or rotating slowly, the reflected light would pass back through the same gap, and the observer would see it.
However, when the wheel rotated at a particular speed, the returning light beam would encounter a tooth rather than a gap, and the observer would see no light. The speed of light, c, could be calculated based on the angular speed of the rotating wheel and the distance to the mirror. The formula Fizeau used is:
c=2dNf
Where:
- c is the speed of light,
- d is the distance to the mirror,
- N is the number of teeth on the wheel,
- f is the frequency of the wheel’s rotation when the light was blocked.
3. Results
Fizeau’s experiment produced a value for the speed of light of about 313,000 km/s, remarkably close to the modern value of 299,792.458 km/s. His method was groundbreaking because it was the first terrestrial, rather than astronomical, experiment to directly measure the speed of light.
Foucault’s Experiment (1850)
Shortly after Fizeau, Léon Foucault developed a more precise technique that refined and improved upon Fizeau’s method by using rotating mirrors instead of a toothed wheel.
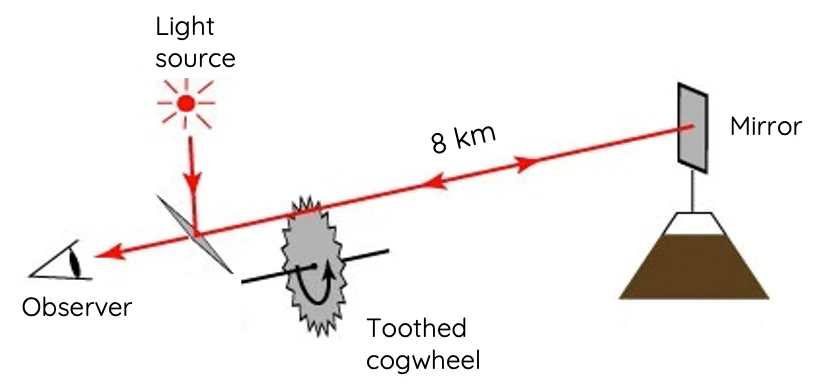
1. Basic Setup
Foucault’s method involved:
- A light source (such as an arc lamp).
- A rotating mirror placed near the light source.
- A fixed mirror placed at a known distance from the rotating mirror.
- A detector to observe the deflection of the light beam.
2. Working Principle
In Foucault’s experiment, light from a source was directed onto a rotating mirror, which reflected the beam toward a fixed mirror located some distance away. After reflecting off the fixed mirror, the beam returned to the rotating mirror and was again reflected back toward a detector. However, by the time the light returned to the rotating mirror, the mirror had moved slightly due to its rotation, so the reflected light was deflected by a small angle.
The deflection angle, combined with the known rotational speed of the mirror, allowed Foucault to calculate the time it took for the light to travel to the fixed mirror and back, thus determining the speed of light. The formula he used was:
Δθ=2ωd/c
Where:
- Δθ is the angular deflection of the light,
- ω is the angular velocity of the rotating mirror,
- d is the distance between the rotating and fixed mirrors,
- c is the speed of light.
3. Results
Foucault’s experiment yielded a value of 298,000 km/s, much closer to the modern value than Fizeau’s. Importantly, Foucault’s method was also capable of measuring the speed of light in different media, such as water, which was critical in verifying the predictions of the wave theory of light.
Refinements of Fizeau and Foucault’s Techniques
As technology advanced, both Fizeau’s and Foucault’s methods were refined. The introduction of better rotating mirrors, improved optical systems, and more accurate distance measurement greatly enhanced the precision of the experiments. One of the most significant refinements was the development of Michelson’s rotating mirror method in 1926, which combined Foucault’s rotating mirror with more sensitive interferometric techniques to achieve much more accurate measurements of the speed of light.
1. Michelson’s Refinements
Albert A. Michelson, who was the first American to win a Nobel Prize in Physics (1907), built on Foucault’s work by employing a similar rotating mirror setup but with greater precision. Michelson’s experiment used longer distances, better optics, and a more carefully controlled rotating mirror system. His experiments, conducted over a baseline of approximately 35 kilometers, determined the speed of light to be about 299,796 km/s.
2. Interference Patterns and Precision
The introduction of interference patterns was crucial in improving the accuracy of these experiments. By splitting a light beam and recombining it after it traveled two different paths, interference patterns could be observed, providing a very sensitive means of detecting small changes in the path length or the speed of light. Interferometry became a powerful tool in precision measurements, including those related to the speed of light.
Technical Discussion: Rotating Mirrors and Interference
1. Rotating Mirrors
The rotating mirror technique works by exploiting the fact that the mirror moves slightly during the time it takes for light to travel from the mirror to a distant point and back. This motion changes the angle at which the light is reflected when it returns to the rotating mirror, and the amount of angular deflection depends on the speed of light.
In Foucault’s experiment, the rotating mirror moved only a small amount during the round-trip time of the light beam, creating a measurable deflection. The higher the mirror’s rotation speed and the greater the distance to the fixed mirror, the more the light beam was deflected. By carefully measuring the deflection angle, Δθ\Delta \thetaΔθ, and knowing the rotation speed, ω\omegaω, and distance, d, Foucault could calculate the speed of light.
2. Interference Patterns
Later refinements using interferometry provided much higher precision by exploiting the wave properties of light. When two light beams traveling different paths are recombined, they interfere, producing constructive or destructive interference depending on their phase difference. Since the phase difference depends on the path length and speed of light, tiny changes in these quantities cause measurable shifts in the interference pattern. This allows extremely accurate measurements of the speed of light by comparing how light travels through different media or across different distances
1. Fizeau’s Setup
A simple diagram of Fizeau’s setup would show:
- A light source shining through a rotating toothed wheel.
- A beam of light traveling to a distant mirror.
- The returning beam encountering a gap or tooth, depending on the wheel’s speed.
2. Foucault’s Setup
A diagram of Foucault’s setup would include:
A slight angular deflection of the beam when it returns due to the rotation of the mirror during the light’s round trip.
A rotating mirror reflecting light toward a fixed mirror.
A beam of light returning to the rotating mirror after being reflected by the fixed mirror.
Interferometric Methods
Modern interferometric methods have revolutionized the precision of measuring the speed of light by using lasers and highly sensitive detectors. Laser interferometry splits a laser beam into two parts that travel along different paths before recombining. The interference pattern generated by the recombined beams reveals tiny changes in the path lengths, which are highly sensitive to variations in the speed of light or environmental conditions. The laser’s coherence and stability provide an extremely accurate measure of the light’s wavelength and phase, enabling distance measurements on the scale of nanometers.
For instance, Michelson interferometers, similar to the ones used in LIGO to detect gravitational waves, measure the relative speed of light over short distances by monitoring phase shifts in the interference pattern caused by minute differences in path lengths. This method is capable of detecting changes in the order of fractions of a wavelength, making it highly accurate for determining light’s speed.
Atomic clocks are essential for precise time-of-flight measurements, which track the time it takes for light to travel a known distance. Atomic clocks use the frequency of electromagnetic radiation emitted or absorbed by atoms, such as cesium or rubidium, to define time intervals with remarkable precision. These clocks operate at microwave or optical frequencies, enabling time measurements on the order of nanoseconds or even picoseconds. By combining atomic clocks with interferometric setups, researchers can accurately measure the time it takes for light to travel very short distances, further refining the value of the speed of light to extraordinary precision.
Defining the Meter in Terms of Light Speed
The General Conference on Weights and Measures redefined the meter in 1983 as the distance light travels in a vacuum in exactly 1/299,792,458 seconds. This section will explore the significance of this definition, the precision involved in the measurement process, and the relationship between time, distance, and the speed of light in modern physics.
Cosmological and Astrophysical Implications
The Speed of Light and the Structure of the Universe
The speed of light, c, fundamentally governs the structure and limits of the observable universe. In relativity, it acts as the maximum speed at which information, matter, or energy can travel, shaping the causal structure of spacetime. This structure is visualized through the concept of a light cone.
A light cone represents all possible light paths emanating from an event in spacetime. The cone is divided into two parts: the future light cone, which encompasses all events that can be influenced by or connected to the original event by signals traveling at or below the speed of light, and the past light cone, which contains all events that could have influenced the original event. Events outside the light cone cannot affect or be affected by the event at its origin, establishing a limit to causality and enforcing the separation of events in spacetime.
The speed of light also sets a limit on the size of the observable universe. Light from the most distant stars and galaxies has taken billions of years to reach Earth, allowing us to observe only objects within a certain radius, known as the cosmic horizon. Given the age of the universe (about 13.8 billion years) and the expansion of space, the observable universe has a radius of approximately 46.5 billion light-years. Objects beyond this distance are not visible because their light has not had time to reach us since the universe’s formation, effectively limiting our observation of the cosmos.
Light Speed and Gravitational Lensing
The speed of light, c, plays a pivotal role in the phenomenon of gravitational lensing, which occurs when a massive object, like a galaxy or cluster of galaxies, distorts the fabric of spacetime around it due to its gravitational field. According to Einstein’s general relativity, massive objects cause a curvature in spacetime, affecting the paths that light takes as it travels through this warped geometry.
When light from a distant galaxy passes near a massive foreground object, the gravitational field of that object bends the light’s trajectory. This bending occurs because the gravitational field alters the space through which the light travels, effectively causing the light rays to follow curved paths rather than straight lines. As a result, the light from the distant galaxy can reach our telescopes even if it would otherwise be blocked or hidden by the foreground object.
Gravitational lensing not only allows us to observe distant galaxies that would be hidden but also enhances our understanding of the universe. The amount of light bending depends on the mass of the lensing object and the distance between the light source, the lens, and the observer. This bending can lead to various observable effects, such as multiple images, arcs, or even rings of light known as Einstein rings.
Additionally, by analyzing the lensing effects, astronomers can infer the mass of the foreground object, including dark matter, which does not emit light and is otherwise difficult to detect. Thus, the speed of light is integral to gravitational lensing, as it governs the relationship between mass, spacetime curvature, and the observable universe.
Event Horizons and Black Holes
The speed of light, c, is crucial to understanding the behavior of black holes and their interaction with spacetime. A black hole forms when a massive star collapses under its own gravity, creating a region where the gravitational pull becomes so intense that not even light can escape. The boundary of this region is called the event horizon. At the event horizon, the escape velocity equals the speed of light, meaning that any object or radiation, including light, falling within this boundary is irreversibly trapped.
The formation of the event horizon is directly tied to general relativity, where Einstein’s equations describe how mass warps spacetime. Near a black hole, this warping becomes extreme, and the curvature of spacetime at the event horizon is so steep that all possible future trajectories point inward, effectively sealing off the interior from the rest of the universe.
The speed of light also plays a key role in black hole thermodynamics. According to Stephen Hawking’s theoretical work, black holes emit a form of radiation—Hawking radiation—due to quantum effects near the event horizon. This radiation is a result of particle-antiparticle pairs forming at the horizon, with one particle escaping and the other falling into the black hole. The temperature of this radiation is inversely proportional to the black hole’s mass, governed by the constants of nature, including c.
Additionally, the speed of light underpins the black hole information paradox, which questions whether information about matter that falls into a black hole is truly lost or encoded on the event horizon. The relationship between the speed of light, quantum mechanics, and spacetime remains central to ongoing debates in black hole physics, especially in reconciling quantum theory with general relativity.
Cosmic Microwave Background Radiation
Light emitted during the early stages of the universe, particularly the cosmic microwave background (CMB) radiation, is crucial for understanding the origins and evolution of the cosmos. The CMB represents the afterglow of the Big Bang, providing a snapshot of the universe when it was approximately 380,000 years old and had cooled enough for protons and electrons to combine and form neutral hydrogen. At this point, photons could travel freely through space, marking the transition from an opaque to a transparent universe.
The CMB is a nearly uniform radiation field that fills the universe and is detected as a faint glow in all directions, characterized by a nearly perfect blackbody spectrum at about 2.7 Kelvin. Studying the CMB allows cosmologists to glean vital information about the universe’s initial conditions, such as its density, temperature fluctuations, and composition. These fluctuations are crucial for understanding the formation of large-scale structures, like galaxies and galaxy clusters.
The finite speed of light is key to the concept of “looking back in time” when observing distant objects in the universe. Since light travels at a constant speed, the light from distant celestial objects takes time to reach us. For instance, if a galaxy is one billion light-years away, we see it as it was one billion years ago. This time delay allows astronomers to construct a chronological picture of the universe’s development by observing various epochs through the light that has reached us from different distances. Thus, the CMB and the finite speed of light enable scientists to piece together the history of the universe, from its explosive beginnings to the formation of galaxies and beyond.


